7

7 5.3. Доказательство теорем геометрии Лобачевского

Аксиоматика геометрии Лобачевского является полной, и поэтому теоремы этой геометрии можно доказывать в любой ее модели. Каждая модель обладает своими специфическими особенностями, которые нужно учитывать при рассмотрении того или иного конкретного вопроса. В данном параграфе приводятся доказательства некоторых теорем геометрии Лобачевского с помощью ее моделей.

Теорема Пифагора

Теорема. Для всякого прямоугольного треугольника плоскости Лобачевского выполняется равенство

ch c = ch a * ch b,

где a, b - длины катетов, c - длина гипотенузы этого треугольника.

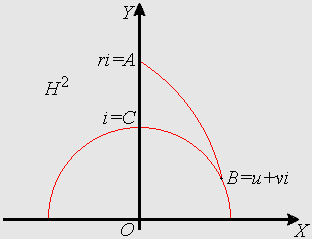
Доказательство. Воспользуемся моделью Пуанкаре H² плоскости Лобачевского на евклидовой полуплоскости. Будем считать (см. рисунок ниже), что вершинам A, B, C данного прямоугольного треугольника соответствуют комплексные числа i, ri, u + vi, где r > 1, u² +v² =1, так как этого всегда можно добиться с помощью некоторого неевклидова движения.

рис. 32

Используя формулу

для вычисления неевклидова расстояния между точками z и w в H², получаем, что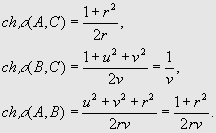

Почленное перемножение двух первых соотношений и приводит, как показывает третье соотношение, к завершению доказательства теоремы.

Замечание к теореме Пифагора

Н.И.Лобачевским было замечено, что созданная им неевклидова геометрия в бесконечно малом, то есть в первом приближении, совпадает с геометрией евклидовой плоскости. Проиллюстрируем это на примере теоремы Пифагора. Используя разложение гиперболического косинуса в ряд

получим для теоремы Пифагора соотношение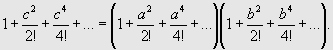

Удерживая теперь члены низшего порядка, приходим к теореме Пифагора евклидовой геометрии:

c² = a² + b²
Площадь треугольника

Для вывода формулы площади треугольника на плоскости Лобачевского вновь обратимся к модели Пуанкаре H² с метрической формой

Пусть ABC - треугольник в H², его площадь S(ABC) мы вычислим как разность площадей треугольников ABD и BCD, где D - бесконечно удаленная точка неевклидова луча AC (см. рисунок ниже).

Найдем площадь треугольника ABD. Меры углов A, B и C треугольника ABC обозначим через a , b и ¡ соответственно, через b ₁ - меру угла B в треугольнике ABD, а через b ₂ и ¡ ₁ меры углов B и C в треугольнике BCD.

Тогда p - ¡ ₁ = ¡ , b 1 - b 2 = b .

Вместо треугольника ABD рассмотрим равный ему в неевклидовом смысле треугольник A₁B_1¥ вершины A₁ и B₁ которого лежат на дуге евклидовой окружности единичного радиуса с центром в начале координат, а третья вершина, обозначенная значком ¥ является бесконечно удаленной. Вычисление площади проведем с помощью формулы, доказываемой в курсе дифференциальной геометрии,

где Q' - область плоскости параметров u, v, соответствующая области Q, а E, F, G - коэффициенты метрической формы поверхности.

Для площади треугольника A₁B_1¥, таким образом, имеем

поскольку в нашем случае

E = G = 1/y², F = 0.

Учитывая расположение точек A₁ и B₁ и то, что их первые координаты равны соответственно cos (p - a ) и cosb ₁ . Получаем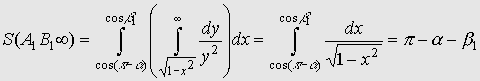

Так как треугольники АВD и A₁B_1¥. Равны, то

S(ABD) = p - a - b ₁

Площадь треугольника BCD можно вычислить таким же образом, при этом

S(BCD) = p - b ₂ - ¡ ₁

Наконец, используя соотношения между углами треугольников ABC и BCD и равенство

S(ABC) = S(ABD) – S(BCD)

получаем искомую формулу для площади данного треугольника:

S(ABC) = p -(a +b +¡ )

Итак, из вышеизложенного вытекает:

Теорема.
Для площади треугольника ABC с углами a b ¡ справедлива формула -

S(ABC) = p -(a +b +¡ )

Следствие1.
Площадь треугольника плоскости Лобачевского ограничена.

Следствие 2.
Если дан выпуклый многоугольник А₁А₂…А_n c внутренними углами a _{1 a
2 a
n} то

S(А₁А₂…А_n ) = (n –2)p - (a _{1 + a
2 + a
n})
Длина окружности и площадь круга

Теорема. Площадь круга радиуса r равна 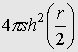а длина окружности, ограничивающей этот круг, равна 2p shr.

Замечание о длине неевклидовой окружности и площади круга

Длина неевклидовой окружности не пропорциональна радиусу, как в случае евклидовой геометрии, а растет быстрее. Также площадь неевклидова круга больше площади круга евклидовой плоскости, имеющего тот же радиус.