2.5. Выполнимость требований аксиом меры для отрезков и углов
Пусть
L - множество всех (неевклидовых) отрезков в H2. Если u, v - две точки в H2, то через s и t обозначим точки, в которых неевклидова прямая uv опирается на ось x в случае, когда uv - полуокружность (надо помнить, что точки оси x не принадлежат H2!). Если неевклидова прямая uv является лучом, то через s обозначим начало этого луча, а t будет его бесконечно удаленной точкой.Покажем, что отображение
l : L
® R+можно определить посредством формулы
l(uv) = c
Ѕ ln(u,v,s,t)Ѕ , (*)где
c - некоторая положительная константа, фиксация которой равносильна выбору единичного отрезка PQ в H2. Рассмотрим сначала случай, когда прямая uv является полуокружностью, при этом числа s и t - действительные, будем считать, что s < t. Через r1 и r2 обозначим модули чисел u - s и u - t, через j 1 и j 2- их аргументы. Поскольку евклидов угол sut - прямой, то![]()
поэтому
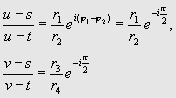
Где
r3 = Ѕ v - sЅ , r4 = Ѕ v - tЅ . Поэтому![]()
В случае, когда неевклидова прямая
uv изображается в H2 лучом, имеем![]()
Таким образом,
(u, v, s, t) > 0, поэтому правая часть равенства (*) имеет смысл и для любого отрезка uv в H2 l(uv) > 0,Покажем теперь, что отображение
l обладает свойством аддитивности, то есть, что для любой точки w отрезка uv выполняется равенствоl(uw) + l(wv) = l(uv).
Действительно, используя соотношения для сложного отношения, получаем, что
(u,v,s,t) = (u,w,s,t)
Ч (w,v,s,t)причем как левая часть данного равенства, так и сомножители правой части этого соотношения положительны. Отсюда имеем, что
ln(u,v,s,t) = ln(u,w,s,t) + ln(w,v,s,t)
Для завершения доказательства аддитивности остается убедиться в том, что слагаемые в правой части последнего соотношения имеют одинаковые знаки. Будем считать для определенности, что точки
u, v, w расположены так, как указано на рисунке ниже.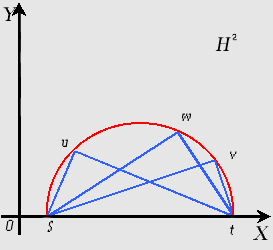
рис.1
Обозначим через
r1, r3, r5 модули комплексных чисел u - s, v - s и w - s, то есть это - евклидовы длины евклидовых хорд su, sv и sw соответственно, поэтому справедливы неравенстваr1 < r5 < r3
Аналогично, если
r2, r4 и r6 - модули чисел u - t, v - t и w - t, тоr4 < r6 < r2
Вычисляя сложные отношения
(u, w, s, t) и (w, v, s, t), получаем равенства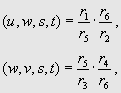
в которых каждый из сомножителей в правых частях меньше единицы в силу приведенных неравенств для
ri, i=1,...,6. Поэтому оба сложных отношения (u, w, s, t) и (w, v, s, t) принимают для рассмотренного случая значения, меньшие единицы. Для остальных случаев расположения точек u, v, w в H2 аналогично вышеизложенному можно показать, что сложные отношения (u, w, s, t) и (w, v, s, t) либо одновременно больше единицы, либо меньше единицы. Поэтому, вычисляя модули обеих частей полученного равенства для логарифмов, получим, чтоЅ
ln(u,v,s,t)Ѕ = Ѕ ln(u,w,s,t)Ѕ + Ѕ ln(w,v,s,t)Ѕ ,отсюда, наконец, учитывая формулу (*), приходим к равенству
l(uv) = l(uw) +l(wv).
Аддитивность функции
l установлена.Устремляя точку
v по неевклидовой прямой uv к точке u, замечаем, что (u, v, s, t) будет стремиться к единице; если же устремлять v к t, то (u, v, s, t) будет стремиться к нулю. Отсюда следует, что в первом случае l(uv) ® 0, а во втором – l(uv) ® Ґ . В то же время l(uv) непрерывно зависит от u и v, следовательно, областью значения для l(uv) является весь интервал (0,+¥ ) то есть все множество R+, а потому при фиксации константы c в формуле (*) найдется такая пара точек P, Q в H2, что значение l(PQ) будет равно единице. Таким образом, фиксируя в формуле (*) постоянную c заранее, мы приходим к выбору отрезка PQ в качестве масштабной единицы. Можно поступить иначе, объявив сначала масштабным некоторый отрезок P1Q1, взять затем значение константы c в формуле (*)так,чтобы получить равенство l(P1Q1) = 1.Итак, требования аксиомы III
1 в H2 выполнены. Заметим, что значение функции l(uv), получаемое с помощью равенства(*), естественно называть также расстоянием между точками u и v.Обратимся теперь к аксиоме III
2. Под градусной мерой ф(pq) неевклидова угла pq будем понимать евклидову градусную меру угла между касательными векторами к сторонам угла pq в его вершине. Ясно, что при таком истолковании градусной меры неевклидова угла требования аксиомы III2 выполнены.