Исторически первая модель была создана Итальянским геометром Эуджинио Бельтрами (1835-1900) в своей работе "Опыт интерпретации неевклидовой геометрии", опубликованной в 1868 г. Он показал, что внутренняя геометрия поверхностей постоянной отрицательной кривизны могла бы служить моделью планиметрии Лобачевского. Поверхности постоянной отрицательной кривизны исследовал еще в 30-е годы XIX в. Фердинанд Миндинг (1806-1885), работавший в Дерптском университете. В 1901 г. Давидом Гильбертом (1862-1943) было доказано, что в трехмерном евклидовом пространстве E³ не существует регулярной поверхности постоянной отрицательной кривизны, изометричной всей плоскости Лобачевского. На имеющихся же в E³ поверхностях постоянной отрицательной кривизны реализуется планиметрия не всей плоскости Лобачевского, а лишь некоторой ее части. Именно такой результат был получен Бельтрами. Исследования Бельтрами имеют большое принципиальное значение. Даже частичная реализация неевклидовой планиметрии в евклидовом пространстве изменила скептическое отношение геометров к работам Лобачевского. Поэтому открытия Бельтрами сыграли важную роль в общем развитии науки.

Пусть плоскость a касается предельной поверхности S в точке O (рис. 14). Проводя через точки плоскости a оси предельной поверхности,мы отобразим

эту плоскость в круг на предельной поверхности с центром О и предельным радиусом OR = s (QQў - ось предельной поверхности, параллельная плоскости a ). Окружность, ограничивающую эту область, мы будем называть абсолютом. Прямые линии плоскости

Рассмотрим пучок 3-го рода U (рис. 15); пусть 0В — прямая этого пучка, проходящая через точку касания О. Рассмотрим пучок плоскостей Т с осью QQ', параллельной прямой 0В и являющейся осью предельной поверхности. Плоскости этого пучка пересекают плоскость a по прямым рассматриваемого пучка 3-го рода U, и обратно - каждая прямая пучка U может быть получена как прямая пересечения плоскости a с некоторой плоскостью пучка Т. В пересечении с предельной поверхностью S плоскости пучка Т дают пучок предельных дуг V с центром R, лежащим на абсолюте.

Покажем теперь, что пучок расходящихся прямых W в плоскости a (рис. 16) дает в отображении пучок

предельных дуг Z, продолжения которых за абсолютом пересекаются в некоторой точке М.

Для доказательства проведем через ось пучка W плоскость b , перпендикулярную к a , и построим ось КК' предельной поверхности, перпендикулярную к плоскости b . Прямая КК' пересекает предельную поверхность в некоторой точке М, лежащей вне абсолюта. Плоскости, проходящие через КК', дают в пересечении с плоскостью a прямые пучка W (ввиду перпендикулярности этих плоскостей к b ), а предельную поверхность пересекают по предельным линиям, проходящим через точку М. Обратно, каждая прямая пучка W может быть получена как пересечение плоскости a с некоторой плоскостью, проходящей через KK'.

Таким образом, факты проективной природы, относящиеся к прямым плоскости Лобачевского, выражаются очень просто на предельной поверхности при указанном отображении. Иначе обстоит дело с метрическими соотношениями. Ясно, что расстояния и углы в плоскости Лобачевского не равны длинам соответствующих предельных дуг и углам между предельными дугами на предельной поверхности. Установим формулы, выражающие расстояния и углы.

Возьмем точки А₁, А₂ в плоскости a (рис. 17); пусть они отображаются в точки А_1ў , А_2ў предельной поверхности S. Введем следующие обозначения-

Имеем (по “теореме косинуса” - )

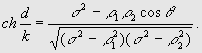
Аналогично выводится формула для угла j между пересекающимися прямыми (рис. 18, слева) и для кратчайшего расстояния 6 между двумя расходящимися прямыми (рис. 18, справа). Пусть ОР₁, ОР₂ - предельные дуги, проведенные из точки О ортогонально к предельным линиям, получающимся при

отображении из прямых плоскости a (точки Р₁ и Р₂ принадлежат соответственно первой и второй из этих предельных линий). Обозначим ОР₁ = s ₁ , ОР₂ = s ₂, угол между дугами ОР₁ и ОР₂ через w . Тогда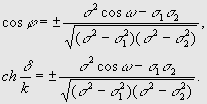

(2)