3.2. Интерпретация Бельтрами.

]
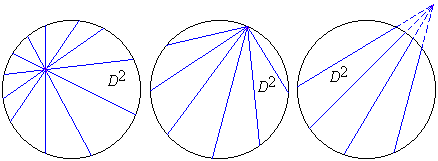
Рис.19 а) б) в)Получив отображение плоскости Лобачевского на предельную поверхность, мы можем построить интерпретацию этой плоскости в плоскости Евклида. Так как на предельной поверхности имеет место евклидова геометрия, то, отображая предельную поверхность на плоскость Евклида, получим
в этой последней следующую интерпретацию. Плоскости Лобачевского соответствует область, ограниченная окружностью (абсолютом) радиуса s (рис. 19); ввиду произвольности выбора единицы длины радиус абсолюта является произвольным отрезком. Прямые плоскости Лобачевского интерпретируются отрезками
рис.20
прямых, лежащими внутри абсолюта. Пучки прямых различного рода изображаются пучками прямых с центрами, лежащими внутри абсолюта (пучки 1-го рода, рис. 19, а), вне (пучки 2-го рода, рис. 19,в
) или на абсолюте (пучки 3-го рода, рис. 19, б). Неевклидовы расстояния, углы и кратчайшие расстояния между расходящимися прямыми определяются соответственно формулами (1), (2) и (3) (см. выше).Вводя вместо полярных координат прямоугольные декартовы координаты с началом
в центре абсолюта (рис. 20), имеем (через x1, y2 и x2, y2 обозначены координаты точек А и В, неевклидово расстояние между которыми равно d)![]() (4)
(4)
Если прямые а, b, интерпретирующие прямые в плоскости Лобачевского, заданы уравнениями
u1x+v1y-w1=0
u2x+v2y-w2=0
то угол
j между соответствующими прямыми на плоскости Лобачевского (в случае пересечения) и кратчайшее расстояние d (в случае расхождения) определяются следующими формулами: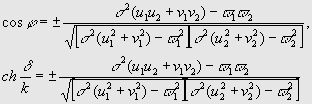 (5)
(5)
Пользуясь этими формулами, нетрудно выразить неевклидовы расстояния и углы при помощи проективных понятий.
Если прямая АВ пересекает абсолют в точках М и N, то
![]() (7)
(7)
где (MNAB) = ![]() - ангармоническое отношение четырех точек M, N, A, B).
- ангармоническое отношение четырех точек M, N, A, B).
Для угла и кратчайшего расстояния между расходящимися прямыми можно вывести аналогичные формулы. Пусть (рис. 20) а, b
— прямые, интерпретирующие две пересекающиеся прямые плоскости Лобачевского, т. е. а, b пересекаются внутри абсолюта. Пользуясь понятиями комплексной геометрии, можно говорить о паре комплексно сопряженных касательных т, п к абсолюту, проведенных из точки пересечения прямых а и b. Из формулы (5) получаем![]() (8)
(8)
Если прямые а, b интерпретируют расходящиеся прямые, то точка их пересечения лежит вне абсолюта;
из нее можно провести две действительные касательные т, n к абсолюту. Формула (6) дает![]() (9)
(9)
Построенная интерпретация плоскости Лобачевского называется интерпретацией Бельтрами. Отметим, что она может быть получена и чисто аналитически. В самом деле, пользуясь координатами Бельтрами, отнесем к каждой точке (х,y) плоскости Лобачевского точку евклидовой плоскости, определяемую прямоугольными декартовыми координатами
x'
=s x, у' = s у.Так как координаты Бельтрами удовлетворяют неравенству
![]() ,
,
то плоскость Лобачевского отобразится в круг радиуса
s .