Уже в первых своих мемуарах, Клейн, опираясь на работу Кэли (суть которой изложена выше), ставит задачу о построении интерпретации неевклидовой геометрии гораздо шире и притом в двух отношениях: во-первых, при воспроизведении плоской двумерной геометрии он не ограничивается группой проективных преобразований инвариантного круга, а рассматривает группу, оставляющую инвариантным любое овальное (т.е. действительное и невырожденное) коническое сечение, во-вторых, он строит модель не только двумерной, но и трехмерной неевклидовой геометрии.

Ограничиваясь сначала геометрией плоскости, Клейн исходит из предложения, которое было известно и до него: каково бы ни было овальное коническое сечение, всегда существует трехпараметрическая группа проективных преобразований плоскости, оставляющих это коническое сечение инвариантным. Это проще всего подтверждается следующими соображениями.

Как известно, точечное проективное соответствие в плоскости вполне устанавливается заданием четырех точек, соответствующих заданным исходным четырем точкам общего положения, т. е. образующим невырожденный четырехугольник (никакие три из вершин не лежат на одной прямой). Проективное соответствие преобразует всякое овальное коническое сечение в овальное же.

При этом любая точка и ее поляра относительно этого конического сечения переходят в полюс и поляру преобразованной кривой; в частности, точка на коническом сечении и касательная к ней переходят в точку преобразованной кривой и касательную к ней в этой точке.

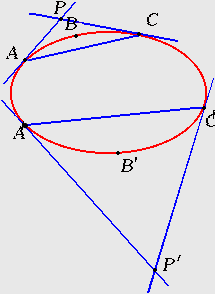
Пусть теперь Ф — некоторое овальное коническое сечение, А, В, С— произвольные три различные точки на нем. Две из этих трех точек (скажем, А и С) соединим, прямой АС', пусть Р будет полюс этой прямой (рис.21) относительно конического сечения (Р есть точка пересечения касательных АР и СР, проведенных в точках A и С). Если проективное преобразование П преобразует коническое сечение Ф в себя само, то оно переводит точки А, В, С в точки А', В', С' того же конического сечения и полюс Р прямой АС в полюс Р' прямой А'С'. Имея это в виду, фиксируем на коническом сечении Ф три точки Л, В, С; вместе с тем окажется фиксированной точка Р—полюс прямой АС. Теперь выберем на Ф произвольные три различные точки А', В', С', которые примем за соответствующие точкам А, В, С; пусть Р' будет полюс прямой А'С' относительно Ф. Четыре точки А', В', С', Р' в качестве соответствующих точкам А, В, С, Р определяют проективное соответствие П. в этой плоскости; оно преобразует коническое сечение Ф в коническое сечение Ф'. Как известно, три точки А', В', С' вместе с проведенными в двух из них (А', С') касательными (А'Р', С'Р') однозначно определяют коническое сечение Ф' (грубо говоря, задание этих элементов равносильно заданию пяти точек: В', одной пары слившихся в А' и другой пары слившихся в С'), поэтому Ф' не может отличаться от Ф. Этим доказано, что преобразование П оставляет коническое сечение Ф инвариантным.

Проективное преобразование П определяется таким образом заданием трех точек А', В', С' конического сечения, как соответствующих фиксированным точкам А, В, С. Но каждая из точек А', В', С' на коническом сечении Ф определяется одним числовым заданием (например, полярным углом в системе, где полюсом служит фокус, а полярной осью—главная ось). Каждое преобразование П таким образом зависит от трех параметров, а совокупность таких преобразований составляет трехпараметрическую группу.

Под внутренней областью конического сечения, как обыкновенно, подразумевают ту часть плоскости, из точек которой нельзя провести действительных касательных к кривой. Ясно, что каждое действительное преобразование П, которое преобразует коническое сечение Ф в само себя, приводит каждую внутреннюю ее точку во внутреннюю же его точку; в самом деле, иначе две мнимые касательные переходили бы в действительные касательные. Овальное коническое сечение может быть принято за абсолют клейновой интерпретации гиперболической геометрии.