4.4. Выражение расстояния между двумя точками в модели Кэли-Клейна при любом овальном абсолюте.
Напишем уравнение конического сечения, служащего абсолютом, в однородных координатах х, у, z в виде
![]() (1)
(1)
К функции Ф (х, у, z) присоединим множитель +1 или — 1 так, чтобы для внутренних точек этого конического сечения было Ф (x, у, г) > 0. Если
M1(x1, y1,z1) и М2(x2,,y2,,z2) две точки внутри абсолюта, то прямую, через них проходящую, можно выразить уравнениями:![]() (2)
(2)
Чтобы разыскать точки, в которых прямая (2) пересекает коническое сечение (1), подставляем выражения (2) в уравнение (
1).Для соответствующего значения ![]() получим уравнение
получим уравнение
![]() (3)
(3)
где Ф
11 и Ф22 суть значения формы Ф в точках x1, y1, z1 и x2,,y2,,z2 а Ф12 есть значение соответствующей билинейной формы:![]() (4)
(4)
Уравнение (3) дает два значения отношения ![]()
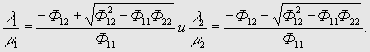
Для двойного отношения пары точек
M1 , М2 и пары точек пересечения , соответствующих найденным для![]() (или
(или ![]() )=
)=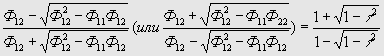 (5)
(5)
![]() (6)
(6)
Поскольку прямая, проходящая через две внутренние точки конического сечения, пересекает его в двух действительных точках, всегда будет ![]()
Общая теорема.
Изложенные соображения могут быть выражены следующей общей теоремой: Какова бы ни была в евклидовой плоскости овальная кривая второго порядка, внутри нее можно построить клейнову интерпретацию гиперболической плоскости; движениями в этой интерпретации служат проективные преобразования, оставляющие это коническое сечение (абсолют) инвариантным (преобразующие его в самого себя). Метрическими величинами служат численные инварианты этих преобразований. Абсолют можно рассматривать как совокупность бесконечно удаленных точек гиперболической плоскости.